前言

本文中出现的动画均使用 Powerpoint 制作，需要源文件的可以私聊分享。

“字符串匹配”是一个传统的算法问题。给定一个文本串 S 和模式串 T，判断 T 是否为 S 的子串。如果是，则返回 T 在 S 中首次出现的位置；如果不是，则返回 -1。

对于这类算法问题，KMP 算法是一种较好的解决方案💡。

🔍下面来看看 KMP 算法的优势：

👎暴力算法演示图：

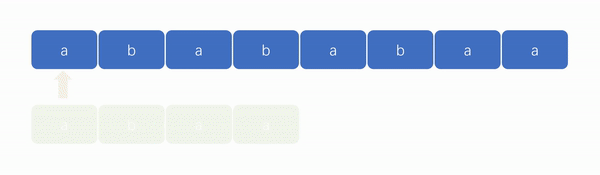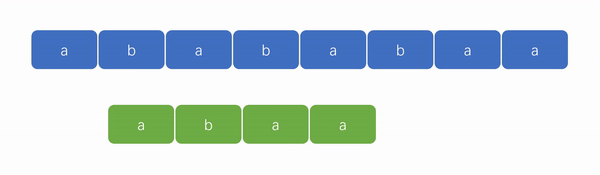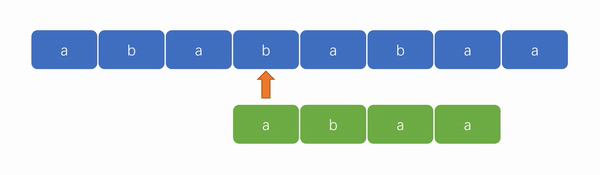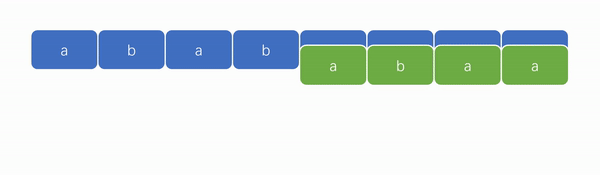
👍KMP 算法演示图：

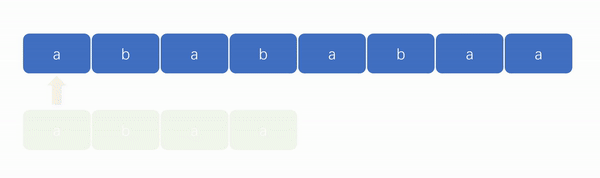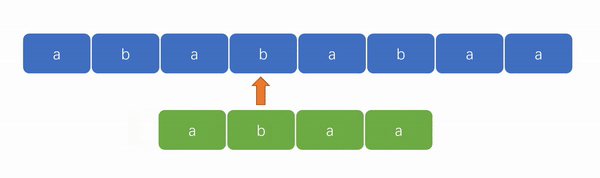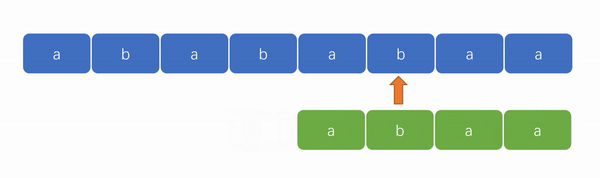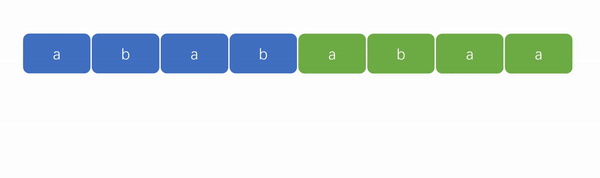
从上面两张演示图中，可以看出 KMP 算法的优势在于“匹配更快”和“遍历指针无需回溯”。


算法介绍

下面是来自百度百科🌐的介绍：

KMP 算法是一种改进的字符串匹配算法，由 D.E.Knuth，J.H.Morris 和 V.R.Pratt 提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称 KMP 算法）。KMP 算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个 next() 函数实现，函数本身包含了模式串的局部匹配信息。KMP 算法的时间复杂度O(m+n) 。

该算法相对于 Brute-Force（暴力）算法有比较大的改进，主要是消除了主串指针的回溯，从而使算法效率有了某种程度的提高。

在分析 KMP 算法前，需要先了解以下名词：

👉文本串：由数字、字母、下划线组成的一串字符。这里指需要被搜索的主串 abababaa。

👉模式串：比主串短的一串字符。这里指用于匹配的字符串 abaa。

👉模式匹配：在文本串中找出和模式串相同的子串。

👉遍历指针：遍历文本串的指针。

1️⃣ 传统暴力算法在每次匹配失败后，都需要从模式串的第一个字符开始匹配。如下图，我们可以看到遍历指针在匹配失败后会出现回溯现象。

2️⃣ KMP 算法的强大之处在于能够避免遍历失败后的指针回溯。如下图，我们可以看到遍历指针只会往后走，变化的只有模式串的匹配位置。

💡 KMP 算法能够避免指针回溯的关键就在 next 数组上。它的思想就是记录已经匹配成功的模式串元素，让当前匹配失败的文本串元素不需要从模式串首元素重新开始匹配，而是从匹配成功的模式串元素的后一个元素开始匹配。

🔖 next 数组能够让我们知道，当文本串元素和模式串元素匹配失败后，应该跳转到模式串的哪个元素重新开始匹配。如下表：

下标 0 1 2 3
元素 a b a a
next 数组 0 0 0 1

例如，当最后一个元素“a”（下标为 3）在匹配失败后，文本串不需要从模式串第一个元素“a”（下标为 0）的位置重新开始匹配，而是到第二个元素“b”（下标为 1）开始匹配。如下图：

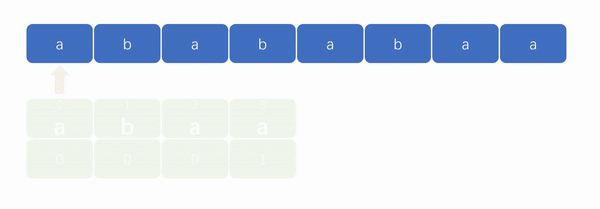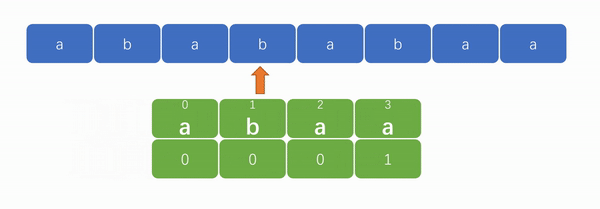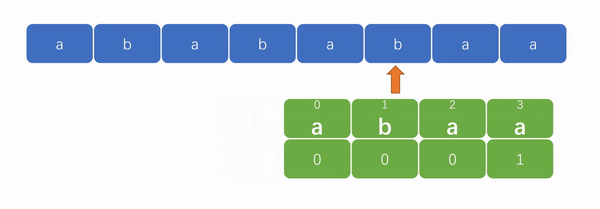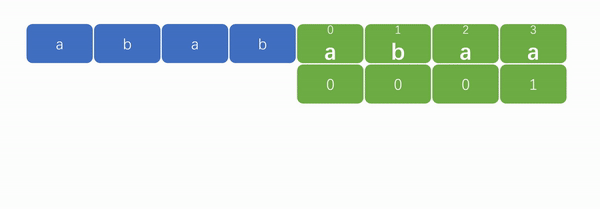
现在只要能够求解出 next 数组，实现“字符串匹配”就不成问题了。


next数组详解

总体分析

给出结论：next 数组除了表示匹配失败后下一次匹配的元素下标，还表示当前下标和整个模式串的共同前缀的长度。

从“next 数组能够让我们知道，当文本串元素和模式串元素匹配失败后，应该跳转到模式串的哪个元素重新开始匹配。”这句话中，我们得出两个结论：

  1. next 数组与模式串有关，那么它的长度应该等于模式串的长度。
  2. 当文本串元素和模式串中下标为 i 的元素匹配失败后，需要获取 next[i] 的值来找到下一次匹配的模式串元素，拿来与当前文本串元素进行匹配。

❓那么，假设现在有模式串 T =“ababaab”，如何求它的 next 数组？

⁉️next 数组能够知道匹配失败后下一次匹配的模式串元素，就说明在此元素之前的元素都是匹配成功的，这样才能避免重新从模式串第一个元素开始匹配。那些匹配成功的元素就是与整个模式串前缀相同的元素，所以也有人叫它“prefix 数组”。

例如，现在有模式串 ababaab，下标为“5”的元素是“a”（橙色），求 next[5] 的值？

从模式串中可以看出，匹配成功的元素（绿色）应该是“ababaab”，与其对应的前缀元素是（红色）“ababaab”。

为了匹配效率，其对应的前缀元素应该是最长的。即在前缀“a”和“aba”中，选择“aba”。

那么，next[5] 的值应该是“3”。因为前面的“aba”是已经匹配成功的元素，所以只要从下标为“3”的元素开始匹配就行。由于数组从 0 开始，那么也说明“3”是匹配成功元素的长度。

❗现在我们就能够得出：next 数组除了表示匹配失败后下一次匹配的元素下标，还表示 当前下标 和 整个模式串 的 共同前缀的长度。（PS：在我看来，这是最容易理解的。）

实现推导

可以选择直接跳到代码实现。

知道 next 数组的具体含义，现在我们回到问题：“假设现在有模式串 T =“ababaab”，如何求它的 next 数组？”。我们可以利用动态规划的思想，将它拆分成一个个子串。不过在此之前需要用一些变量来表示它们。

👉 指针“i”用来遍历的模式串元素，即 next[i] 中的“i”。（橙色）

👉 指针“j”指向共同前缀的后一个元素（待匹配元素）。“j”指针前面的元素都是已经匹配成功的共同前缀。作用是找共同前缀。具体用处看下面的推导……

  1. “a”：i = 0，整个模式串只有一个元素时，匹配失败直接继续匹配即可，即 next[0] = 0。

  2. “ab”：i = 1，整个模式串只有两个元素时，如果“a”匹配成功、“b”匹配失败，那么说明当前 i 下标指向的元素需要重新从“a”开始匹配，即 next[1] = 0。

  3. “aba”：i = 2，整个模式串有三个及以上数量的元素时，这时候在“首元素”和“当前匹配元素”中就有其他元素，也就意味着存在不需要从“首元素”开始匹配的可能。那么我们让“j = 0”即指向“首元素 a”。那么就可以开始找共同前缀了。我们直接把 T[j] 和 T[i - 1] 进行比对，一个是整个模式串的前缀，一个是当前下标的前缀。T[j] != T[i - 1] 说明它们不是共同前缀，此时共同前缀的长度为 0，即 next[2] = 0。

  4. “abab”：i = 3，这时候还不存在共同前缀，那么就意味着我们还需要从“j = 0”开始找共同前缀。此时T[0] == T[2]，说明存在共同前缀“a”。即 next[3] = 1。

  5. “ababa”：i = 4，这时已经存在一个共同前缀“a”，说明“j”需要后移一位“j = 1”，判断第二位是否也属于共同前缀。此时 T[1] == T[3]，说明存在共同前缀“ab”。那么 next[4] = 2。

  6. “ababaa”：i = 5，这时的共同前缀为“ab”、j = 2，由于 T[2] == T[4]，即 next[5] = 3。

  7. “ababaab”：i = 6，这时的共同前缀为“aba”、j = 3。前面都是匹配成功的例子，如果出现匹配失败该怎么办？继续往下看。此时 T[3] != T[5]，说明当前共同前缀已被推翻，需要获取新的共同前缀。

    如下图，此时“b”不等于“a”。但是 next 数组中储存有“b”的共同前缀。next[3] = 1，说明它共同前缀的长度为 1 且匹配失败后下一个要匹配的元素的下标为 1。让 j = 1，继续开始匹配。此时“b”不等于“a”。继续回溯，j = 0，此时“a”等于“a”，说明公共前缀有 1 个，即 next[6] = 1。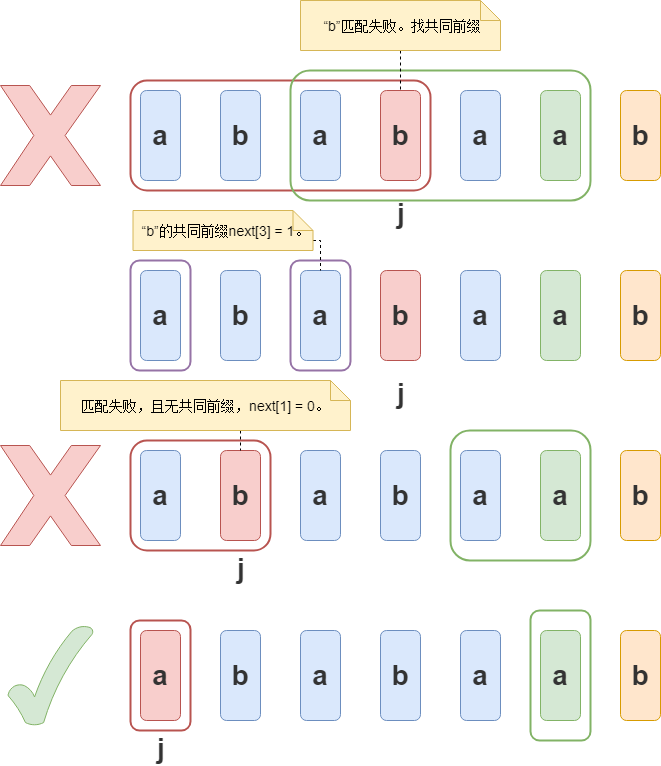

求出模式串 T =“ababaab”的 next 数组为：

下标 0 1 2 3 4 5 6
元素 a b a b a a b
next 数组 0 0 0 1 2 3 1

next 数组的推导视频如下：

🚫暂时无法播放…

代码实现

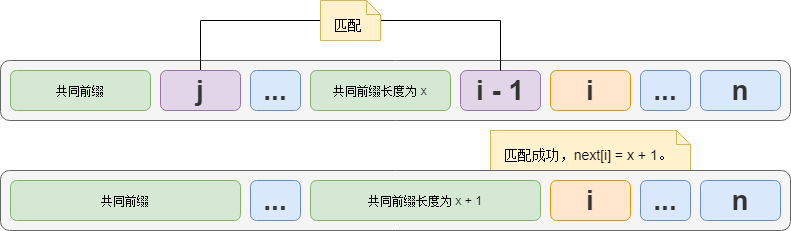
✅在匹配成功的时候，直接将共同前缀的长度加 1 即可。共同前缀的长度是指针“j”的值。如下图：

❎在匹配失败的时候，就需要考虑边界了。如下图：

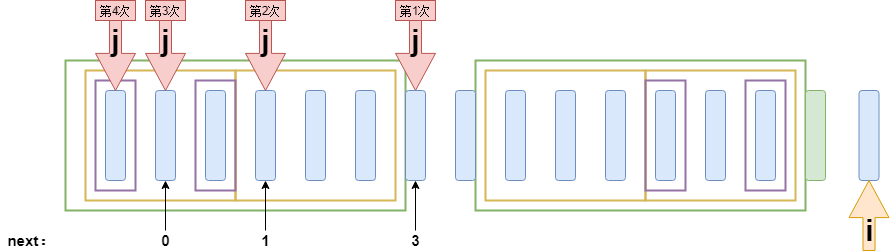
0️⃣如果只是正常的回溯并没有什么问题，直接让指针“j”指向下一个要匹配的元素（j = next[j]）。匹配成功后将共同前缀的长度加 1 即可。

例如，在第一次匹配失败时，需要“j”指针回溯，回到“j”元素的共同前缀的后一位元素的位置（next[j] = 3）。“j = 3”进入第二次匹配，如果匹配成功。此时共同前缀的长度是 3，所以 next[i] = 3 + 1 = 4。

1️⃣如果是当“j”指针无法再回溯时，出现匹配失败的情况，就说明当前“i”元素已经没有共同前缀了，即 next[i] = 0。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * 求next数组
 * 
 * @param pattern 模式串
 * @return next数组
 */
public int[] getNext(String pattern) {
    int len = pattern.length();
    if (len <= 1) {
        return new int[]{0};
    }
    int[] next = new int[len];
    next[0] = 0;
    int i = 1, j = 0;
    while (i < len) {
        // 第二个元素都是“0”
        if (i == 1) {
            next[i] = 0;
            i++;
            continue;
        }
        // 匹配成功
        if (pattern.charAt(i - 1) == pattern.charAt(j)) {
            next[i] = j + 1;
            i++;
            j++;
            continue;
        }
        // 匹配失败 
        if (j == 0) {
            // 特殊情况，j == 0，指针无法回溯。
            next[i] = 0;
            i++;
        } else {
            j = next[j];
        }
    }
    return next;
}

✨求 next 数组的代码是实现了，但是不够优雅，感觉还能再简洁一点。所以就有人想出从“j = -1”开始，那么 next[0] = -1。这样做的好处是“匹配成功”、“匹配失败且 j == 0”和“i == 1”的情况可以统一处理。只是需要在使用时，将“-1”看作“0”，防止下标越界。

  • 当“匹配成功”时： next[i] = j + 1、i++、j++。
  • 当“i == 1”或“匹配失败且 j == 0”时：这两种情况可以归结为“j == -1”，因为它们的最终结果都是 next[i] = 0、j = 0、i++，都满足 next[i] = j + 1 = 0、i++、j++。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * 求next数组
 *
 * @param pattern 模式串
 * @return next数组
 */
public static int[] getNext(String pattern) {
    int len = pattern.length();
    if (len <= 1) {
        return new int[]{0};
    }
    
    int[] next = new int[len];
    next[0] = -1;
    int i = 1, j = -1;
    while (i < len) {
        if (j == -1 || pattern.charAt(i - 1) == pattern.charAt(j)) {
            next[i] = j + 1;
            i++;
            j++;
        } else {
            j = next[j];
        }
    }
    return next;
}

求出 next 数组，就可以直接使用 KMP 算法，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public int kmp(String haystack, String needle) {
    int[] next = getNext(needle);
    // kmp算法
    int n = haystack.length();
    int m = needle.length();
    for (int i = 0, j = 0; i < n; i++) {
        // 匹配失败，找next，直到匹配成功。除非“j=0”，即第一个元素就匹配失败。
        while (j > 0 && haystack.charAt(i) != needle.charAt(j)) {
            // 适配next数组存在-1的情况。
            j = next[j] == -1 ? 0 : next[j];
        }
        // 匹配成功
        if (haystack.charAt(i) == needle.charAt(j)) {
            j++;
        }
        // 全部匹配完，那么j指针已经遍历完模式串，直接返回时第一个匹配项的下标。
        if (j == m) {
            return i - m + 1;
        }
    }
    return -1;
}

nextValue数组详解

next value 数组是对 next数组 的优化，主要就是减少无效回溯的次数。对比图如下表：

下标 0 1 2 3 4 5 6
元素 a b a b a a b
next 数组 -1 0 0 1 2 3 1
nextValue 数组 -1 0 -1 0 -1 3 0

如何减少无效回溯的次数，如下图：

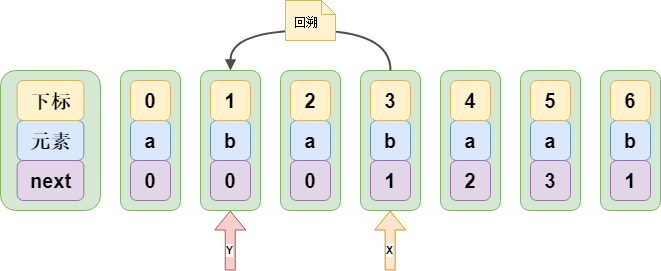
当“X”指针指向的元素匹配失败需要回溯时，它需要回到“Y”指针指向的元素再进行匹配。但是我们可以看出“X”和“Y”指针指向的元素都是“b”，那么说明这是一次无效匹配，它依旧会匹配失败。next value 数组就是对这种情况进行优化。

既然知道“Y”指针指向的元素照样会匹配失败，那就跳过“Y”，直接拿“Y”的 next 值“0”继续匹配。那么原来需要回溯两次，现在只需要回溯一次。

代码实现如下：

从上面可以得出，next value 数组就是根据 next 数组的值，判断回溯的元素和当前元素是否相同？相同则跳过本次回溯；不同则保留原始 next 值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * 求next value数组
 *
 * @param pattern 模式串
 * @return next value数组
 */
public int[] getNextValue(String pattern) {
    int len = pattern.length();
    if (len <= 1) {
        return new int[]{0};
    }
    int[] next = new int[len];
    next[0] = -1;
    int i = 1, j = -1;
    while (i < len) {
        if (j == -1 || pattern.charAt(i - 1) == pattern.charAt(j)) {
            // 在获取next值时，做一次优化。如果当前元素和回溯元素相同，则跳过本次回溯。
            next[i] = pattern.charAt(i) == pattern.charAt(j + 1) ? next[j + 1] : j + 1;
            i++;
            j++;
        } else {
            j = next[j];
        }
    }
    return next;
}

例题训练

题目要求

难度：中等 | LeetCode | 🔗链接直达

给你两个字符串 haystack 和 needle，请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标（下标从 0 开始）。如果 needle 不是 haystack 的一部分，则返回 -1 。

示例 1：

1
2
3
4
输入：haystack = "sadbutsad", needle = "sad"
输出：0
解释："sad" 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ，所以返回 0 。

示例 2：

1
2
3
输入：haystack = "leetcode", needle = "leeto"
输出：-1
解释："leeto" 没有在 "leetcode" 中出现，所以返回 -1 。

提示：

  • 1 <= haystack.length，needle.length <= 104
  • haystack 和 needle 仅由小写英文字符组成

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Solution {
    public int strStr(String haystack, String needle) {
        int[] next = getNextValue(needle);
        // kmp算法
        int n = haystack.length();
        int m = needle.length();
        for (int i = 0, j = 0; i < n; i++) {
            // 匹配失败，找next，直到匹配成功。除非“j=0”，即第一个元素就匹配失败。
            while (j > 0 && haystack.charAt(i) != needle.charAt(j)) {
                j = next[j] == -1 ? 0 : next[j];
            }
            // 匹配成功
            if (haystack.charAt(i) == needle.charAt(j)) {
                j++;
            }
            // 全部匹配完，那么j指针已经遍历完模式串，直接返回时第一个匹配项的下标。
            if (j == m) {
                return i - m + 1;
            }
        }
        return -1;
    }

    /**
     * 求next value数组
     *
     * @param pattern 模式串
     * @return next value数组
     */
    public int[] getNextValue(String pattern) {
        int len = pattern.length();
        if (len <= 1) {
            return new int[]{0};
        }
        int[] next = new int[len];
        next[0] = -1;
        int i = 1, j = -1;
        while (i < len) {
            if (j == -1 || pattern.charAt(i - 1) == pattern.charAt(j)) {
                // 在获取next值时，做一次优化。如果当前元素和回溯元素相同，则跳过本次回溯。
                next[i] = pattern.charAt(i) == pattern.charAt(j + 1) ? next[j + 1] : j + 1;
                i++;
                j++;
            } else {
                j = next[j];
            }
        }
        return next;
    }
}


📌最后：希望本文能够给您提供帮助，文章中有不懂或不正确的地方，请在下方评论区💬留言！

🔗参考文献：

🌐 kmp算法 –百度百科

▶️ bilibili - KMP算法之求next数组代码讲解；甩手掌柜凡三岁. –凡三岁爱学习